• Binary Search
  • Explanation
  • Code
  • Properties
  • Advantages
  • Disadvantage

Binary Search

• Binary search algorithm finds a given element in a list of elements with O(log n) time complexity where n is total number of elements in the list.
• Binary search is applied only on monotonic functions,values should either be in increasing order or decreasing order.
• Binary search can not be used for a list of elements arranged in random order.

Explanation

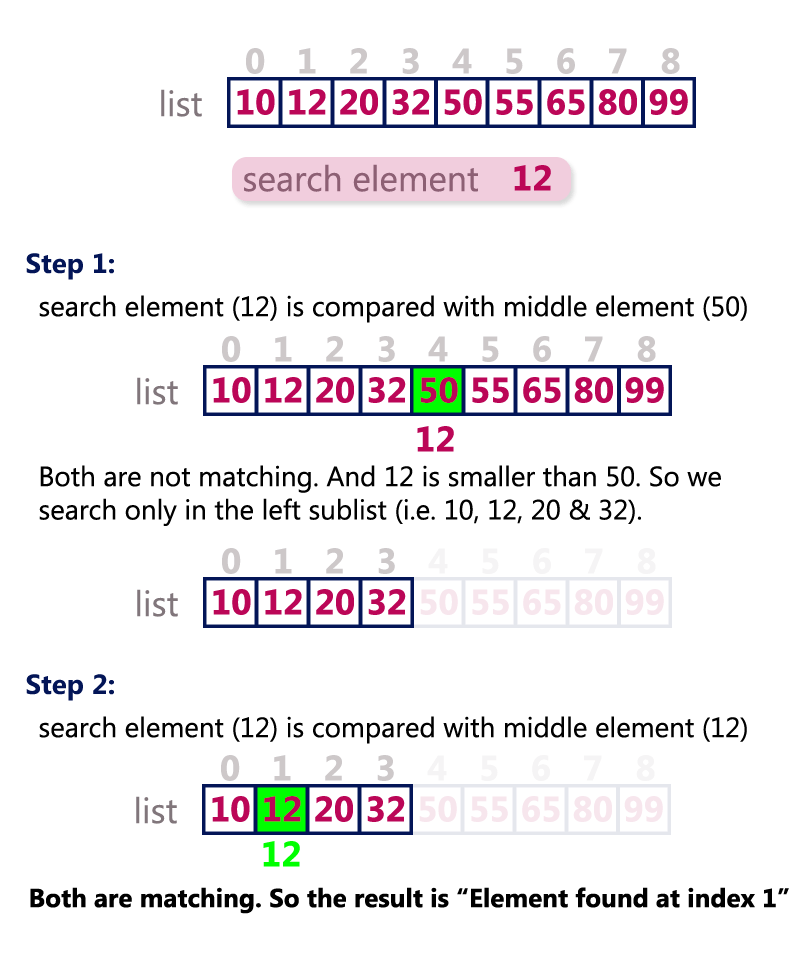
• This search process starts comparing the search element with the middle element in the list. If both are matched, then the result is "element found and we return the index".
• Otherwise, we check whether the search element is smaller or larger than the middle element in the list, then we decide which part we should search.
• If the search element is smaller, then we repeat the same process for the left sublist of the middle element.
• If the search element is larger, then we repeat the same process for the right sublist of the middle element.
• We repeat this process until we find the search element in the list or until we left with a sublist of only one element.
• And if that element also doesn't match with the search element, then the result is "Element not found in the list".

middle = lowerBound + ( upperBound - lowerBound ) / 2

why we are calculating the middle index this way, we can just simply add the lower and higher index and divide it by 2.
 middle = ( lowerBound +  upperBound ) / 2

But if we calculate the middle index like this it fails for larger values of int variables low and high. Specifically, it fails if the sum of low and high is greater than the maximum positive int value(2^31 – 1 ).

Example :

Code

   A ← sorted array
   n ← size of array
   x ← value to be searched

   Set lowerBound = 1
   Set upperBound = n 

   while x not found
      if upperBound < lowerBound 
         EXIT: x does not exists.

      set middle = lowerBound + ( upperBound - lowerBound ) / 2

      if A[midPoint] < x
         set lowerBound = midPoint + 1

      if A[midPoint] > x
         set upperBound = midPoint - 1 

      if A[midPoint] = x 
         EXIT: x found at location midPoint
   end while

end procedure

Properties

• Time Complexity : O(log n)
• Space complexity : O(1)

Advantages

• It is great to search through large sorted arrays.
• It has a simple implementation.

Disadvantage

• The biggest problem with a binary search is that you can only use this if the data is sorted into an order.